Az igazolás elvét sokan ismerik Occam borotvája név alatt. Sokan ismerik, hogy ez az elv azt mondja ki, hogy csak az olyan dolgok létezését szabad elfogadni, amelyek létezése igazolt. Akik erre az elvre hivatkoznak, általában evidensnek veszik, hogy ez az elv miért jó, miért szükséges, miért helyes, miért ésszerű. Ezért ritkán magyarázzák ezt el. A hívők pedig általában nem fogadják el ezt az elvet, sőt, néha azt mondják, hogy az Occam borotvája maga is csak egy igazolatlan hit. Emiatt fontos elmondani, miért is fontos ez az elv, és miért nem egy hit. Egy elv egyébként sem lehet hit, hiszen semminek a létezését vagy nem létezését nem állítja konkrétan, hanem csak egy elv az elméletek elfogadására. Egy ilyen elv lehet praktikus, gyümölcsöző; illetve hátrányos vagy működésképtelen. Az Occam borotvája pedig szükséges, praktikus elv. Ezt egy példával illusztrálom.
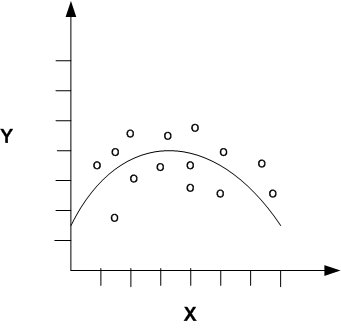
Mesterséges intelligencia kutatóként dolgozom, és ennek során nagyon sokszor ú.n. klasszifikációs vagy regressziós feladatokat kell megoldani. A regressziós feladatot a laikus olvasó könnyebben megérti, és egyváltozós függvényekkel a legkönnyebb elképzelni, ezért ezt a didaktikus példát választom. Képzeljük el, hogy vannak bizonyos adataink, amelyek adatpárokból állnak. Vannak különféle x értékek, és hozzá tartozó y értékek. Ha ezt koordniáta-rendszerben ábrázoljuk, akkor adva vannak egy 2 dimenziós síkon pontok, különféle x és y értékekkel. A regressziós feladat az, hogy ezekre a pontokra egy függvényt illesszünk. Általában azért, mert azt feltételezzük, hogy a pontjaink egy valódi függvényből vett minták, esetleg bizonyos hibával, azaz zajjal.
Különféle nagyon jól kidolgozott regressziós módszerek mellett van egy elméletileg nem olyan jól megalapozott, de praktikus szempontból nagyon jó kis eszköz, amelyet Eurekának neveznek, egy bizonyos Nutonian Team fejlesztette, és ezt sokszor használtam. Ez a program különféle elemi műveletekből és más függvényekből próbálja összerakni azt a függvényt, amely jól illeszkedik a pontokra. Tehát ha például a 4sin(x-2)+3 függvényből vannak a mintáink, és még ha egy kis hiba is van benne, akkor is jó eséllyel a program megtalálja a 4sin(x-2)+3 függvényt. Ezt úgy csinálja, hogy a legegyszerűbb függvényekből kiindulva próbálgat mindenféle variációkat. Az algoritmus az evolúcióhoz hasonló, de ez most itt másodlagos (annak ellenére, hogy az evolúció-kreacionizmus vita is fontos az ateizmus-vallás vita szempontjából).
Ami itt fontos, az az, hogy az összes lehetséges függvényt nem lehet kipróbálni. Ezért a program az egyszerű függvényektől indulva a bonyolultabbak felé haladva keresi a megoldást. Csak akkor fogad el egy bonyolultabb függvényt, ha az jobban beválik (lehetséges, hogy a szelekció nem determinisztikus, de ezt most hanyagoljuk el). A program kénytelen így eljárni, mert nincs más módszer a megoldás megtalálására. Lehet kicsit variálni az algoritmuson, de alapjában nincs más működő algoritmus. Minden algoritmusnak, amely működik, tartalmaznia kell egy olyan elvet, amely kezdőpontot, és keresési irányt jelöl ki a függvények végtelen terében, és olyat is, amelyik részlegesen lekorlátozza, irányítja a keresést. Mert minden függvényt az ember vagy egy algoritmus nem tud áttekinteni. Muszáj az egyszerűbb megoldásokat preferálni, és a bonyolultabb hipotéziseket büntetni.
Teljesen hasonló az elv, amikor a megfigyeléseinkre, mint adatokra illesztünk hipotéziseket, ami a tudomány, vagy általában a megismerés feladata. Ott sem lehet áttekinteni minden hipotézist, ott is az egyszerűbbektől kell kezdeni, és a feleslegesen bonyolultakat kerülni kell. Ezt fogalmazza meg az Occam borotvája elv, amely nem egy alaptalan hit, hanem egy szükséges módszerbeli elem. Enélkül az elem nélkül emberi megismerés nem működhet, mivel végtelen hipotézist nem tudunk áttekinteni.
Ha a hívők erre azt mondják, hogy az istenről szóló hipotézis nem szükségtelenül bonyolult, akkor a válasz az, hogy de bizony, hiszen a tudomány nem tarja szükségesnek ezt a hipotézist: “Erre a hipotézisre nem volt szükségem, Uram”. A hipotézis tehát szükségtelen ahhoz, hogy az adatokra függvényt illesszünk. Nélküle is van jó elméletünk, és ő sem javít az illeszkedésen.
Szakembereknek megemlítem még, hogy ismeretes az univerzális approximációs tétel, amely szerint (neurális hálózatokban) megfelelően gazdag bázisfüggvény-rendszerben bármilyen pontokra, bármilyen pontossággal lehet illesztést találni. Másrészről az overfitting jelensége is ismert, amely szerint a túlságosan pontos illeszkedésnek az általánosítási képessége nem megfelelő, és ezért az ilyen illesztés kerülendő. A jó illesztés és az overfitting elkerülésének kiegyensúlyozása érhető el azzal, hogy a függvény bonyolultságát büntetjük.
Ha a tudományra és a vallásokra használjuk ezt az analógiát, akkor azt mondhatjuk, hogy nem jó az, ha az egyes megfigyeléseinket túlságosan részletesen meg akarjuk magyarázni. Példaként itt az hozható fel, amikor véletlen egybeesésekre gyártanak a vallásosok vagy ezoterikusok hipotéziseket. Ezekből a véletlen egybeesések szükségszerűen szerepel valamennyi az adatainkban, de ha ezekre szükségtelenül valamilyen hipotézist építünk, akkor felesleges és rossz elméleti konstrukciók jönnek létre. Például nemrégiben Czeizel Endre meggyógyult egy rákos betegségből, és ezt ő kivételes szerencsének érezte. Ha erre valamilyen olyan elméletet gyárt, hogy neki védőangyala van, vagy ez isteni csoda, akkor ez az elmélet egy szükségtelen bonyolult elképzelés, mert azért simán belefér az, hogy Czeizel Endrének szerencséje volt. Olyan sokaknak sajnos nincs szerencsére egy ilyen terápia során. A feleslegesen bonyolult elmélet másoknál hamis reményt fog ébreszteni, és ha megnézzük az összes statisztikát, akkor bizony jelenleg is cáfolt. Ezért is fontos elv az Occam borotvája.





