Akármerre járjak, nézzek,
Mindenütt szép a természet,
Szóval ki nem mondható:
Szemnek, szívnek vidítója,
Oh áldott az alkotója,
Isten, a Mindenható.
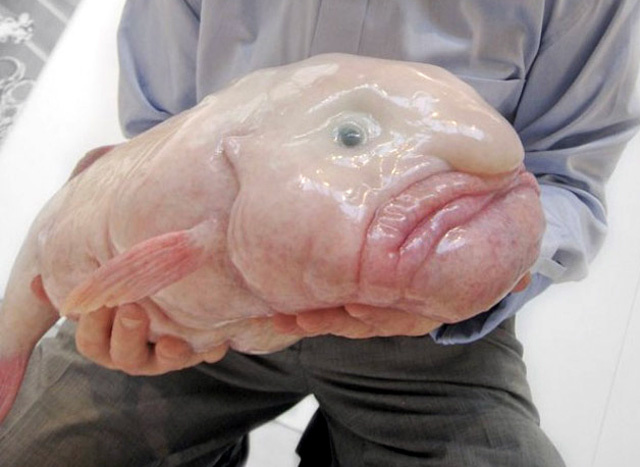
A blugyhalat választották idén a legrondább állat kitüntetett címére. Nem tehetek róla (dehogynem:), de erről nekem a szépségből vett istenérv jutott eszembe. Állítólag már Kant is pedzegette, hogy a szépség szubjektív, emberi dolog, és ha sok mindent szépnek is látunk, az csak azért van, mert evolúciósan (Kant persze nem így fogalmazott) szépnek "tanultuk meg" látni. És sok veszélyes, rossz vagy szokatlan dolgot pedig rondának látunk, mert így "tanultuk meg", vagy nem tanultuk meg, és kiakad rajtuk az esztétikai központunk. Egyébként meg nem kell ezen a halon annyira röhögni, van ember is ilyen ronda, és hát még milyen rondák lehetnek az emberek más élőlények számára!
De mindig akadnak olyanok, akik mégis komolyan veszik a szubjektív esztétikát, főleg tudósok, főleg elvarázsolt pillanataikban. A következőt állítólag Arthur Peacocke, molekuláris biológus írta vagy mondta:
„Ifjúságomban agnosztikus lettem. De roppant hatást tett rám, amikor kutattam, hogy a világegyetem valójában megérthető. Miért bizonyul a természet mindig értelmesen összefüggőbbnek, mint bármi, amit fel tudunk fogni, mielőtt tanulmányokba kezdenénk? Hiszem, hogy a világegyetem ésszerű, mert szuperértelmes lény van mögötte. Megborzongtat a világegyetem szépsége és ésszerűsége, a kvarkoktól az emberi agyig, annak rendje, bonyolultsága és integráltsága. Hiszem, hogy Isten a végső realitás. Isten örök, téren és időn túli.”
Nehéz megmondani, mert manapság az internet tele van hamis idézetekkel, amelyeket másolgatnak, és a megbízható forrásokat, hivatkozással már nem lehet megtalálni. De nem is fontos, mert temérdek hasonló gondolat van, és a Bibliában is fél tucatnyi olyan zsoltár, amely áldja a természet szépségéért az úrat.,
Viccelődve mondhatám, hogy talán nem csak Peacocke volt elvarázsolva, hanem isten a blugyhalat a lélek egy sötét, delíriumos teadélutánján teremtette, amikor megcsalta a felesége Thorral.:) Van ebben az egész történetben, a nevetségességében és a halasságában valami douglas adamsi irónia.
No, a végén legyen valami kemény érv is! Swinburnet valamiért nem közösítették ki az analitikus filozófiából, hanem félig-meddig komolyan veszik, holott a hülyeségeivel keményen megdolgozik azért, hogy ne vegyék. Ő képes komolyan érvet csinálni az Univerzum szépségből, amelyről az imént már elmondtam, hogy szubjektív, és hát demonstráltam, hogy kétséges, mint "tény". De azért ő nyomja. Az alábbi módon érvel a Wikipédia-oldalon idézett könyvben. És most nem idézem, hanem csak a képleteket írom:
legyek k a rendezett Univerzum létezésének eseménye
legyen e a szép Univerzum létezésének eseménye
legyen h isten létezésének eseménye
legyen P(h|e) a feltételes valószínűség jele (itt eltértem Swinburne jelölésétől, hogy az osztás jelével ne keverjük)
legyen P(h|e.k) azon feltételes valószínűség jele, hogy létezik isten, feltéve, hogy az univerzum rendezett és szép
Swinburne érve:
P(e|h.k) jóval nagyobb, mint P(e|k). Great. Ez szép, hatásvadász "érv", csak ugye nem ez a kérdés, nem ez az, amit meg kell kérdeznünk, nem ez a kérdés az, ami döntő. Amit kérdeznünk kell, mit következtethetünk isten létezésének valószínűségéről abból, hogy "szépnek" találjuk az Univerzumot? Mit mondhatunk isten létezésének valószínűségéről abból, hogy megfigyeljük, az Univerzum "szép"? Namost, mivel Swinburne valamiért a rendezett Univerzumot is belekeverte, ezért ezt benne hagyjuk a képletben. Bayes tételéből tudjuk, hogy:
P(h.k|e)=P(e|h.k)P(h.k)/P(e)
itt P(e) egy 0 és 1 közötti, ismeretlen szám. P(h.k) ismeretlen szám, egy ateista szerint simán nulla. P(e|h.k) egy 0 és 1 közötti szám, igazából ezt meghatározhatja a hívő, elfogadhatjuk, hogy lehet akár 1 is. Ebből következően P(h.k|e) vagy 0 vagy 0/0 alakú. Azaz megy az istenérv a levesbe. Akik még tovább akarják vinni ezt az ab ovo hülyeséget. Kérdezheti valaki azt, hogy ha látjuk, hogy az Univerzum rendezett és szép, akkor mennyi isten létezésének valószínűsége?
P(h|k.e)=P(k.e|h)P(h)/P(k.e), megint 0 vagy 0/0 alakú.
Vagy próbáljuk meg k nélkül!
P(h|e)=P(e|h)P(h)/P(e), szintén 0 vagy 0/0 alakú.
Vagy próbáljuk meg k-val, de az eredményben küszöböljük ki k-t!
P(h|e)=P(h.k|e)/P(k|h.e)=P(e|h.k)P(h.k)/P(e)/P(k|h.e), és P(k|h.e)-t megint vehetjük 1-nek, vagy 1 közeli számnak, akkor megint 0, vagy 0/0 alakú eredmény jön ki.
Mindig az a baj, hogy isten a priori valószínűségéről, P(h)-ról nem tudunk semmit, illetve simán mondhatjuk azt, hogy 0.És köznapi szavakkal elmondva, azt mondhatjuk, hogy bár egy rendezett vagy szép Univerzum relatíve növeli isten létezésének feltételes valószínűségét, de ha eleve totál valószínútlen ez a hipotézis, akkor nem érünk vele semmit. Kicsit növelni a nullát, vagy a nagyon keveset, az nem elég.
Egyébként ugyanez a hiba a finomhangoltságból vett istenérvvel is, és minden más istenérvvel, amely feltételes valószínűségekkel operál. Az a baj, hogy isten a priori valószínűségéről nem mondhatunk semmit, ismeretlen, simán mondhatja az ateista, hogy szerinte nulla. Erre rámutattam már a Magyar Tudományban megjelent cikkemben is.
És ismétlem, a szépségből vett istenérv a finomhangolásból vett istenérvnél is bugyutább, mert még szubjektívebb a kiindulópontja.